OPTIMAL TIMING STRATEGIES IN BLOCKCHAIN BLOCK PROPOSALS BY ONE-BULLET SILENT DUELS WITH ONE-THIRD PROGRESSION

Abstract

Background. Silent duels and related timing games offer a surprisingly deep lens into certain core challenges in blockchain technology, especially when it comes to block proposal timing. Miners or validators effectively “compete” in a race to propose the next block. The success of a block proposal depends not only on when it happens but also on whether others have already succeeded or interfered — very much like the tension in a one-shot duel with uncertain outcomes. In block proposal timing for decentralized consensus protocols, a one-shot timing game models a blockchain setting, where participants (e. g., validators or miners) choose when to attempt block proposal or transaction insertion under uncertainty.

Objective. The paper aims to determine the best timing strategies for the participants. Considering two identical participants, the local objective is to find pure strategy solutions of a timing game (duel) with shooting uniform jitter.

Methods. A finite zero-sum game is considered, which models competitive interaction between two subjects to make the best discrete-time decision by limited observability. The moments to make a decision (to take an action, to shoot a bullet) are scheduled beforehand, and each of the subjects, alternatively referred to as the duelists, has a single bullet to shoot. Shooting is only possible during a standardized time span, where the bullet can be shot at only specified time moments. In the base pattern, apart from the duel beginning and final time moments, every following time moment is obtained by adding the third of the remaining span to the current moment. However, the precise time moment specification is not always realizable (e. g., due to the distance between neighbouring time moments being measured with finite accuracy) and so the internal moments are uniformly jittered. This means that they can be slightly shifted within the duel span. The duelist benefits from shooting as late as possible, but only when the duelist shoots first. Both the duelists act within the same conditions by linear shooting accuracy, and so the one-bullet silent duel is symmetric, regardless of the jitter. Therefore, its optimal value is 0 and the duelists have the same optimal strategies, although they still can be non-symmetric.

Results. By the one-third progression pattern with jitter, the 3 x 3 duel always has a pure strategy solution. The 4  x 4 duel is pure strategy solvable by any possible jitter except for jitter interval 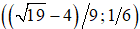. Within this interval and interval (-11/54; -1/18) the 5 x 5 duel is pure strategy non-solvable. The 6 x 6 duel is pure strategy solvable by any possible jitter except for jitter intervals  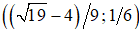and (-49/162; -1/18). Duels with seven to nine time moments are pure strategy solvable only by a jitter interval of 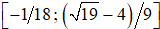. Bigger N x N duels, having no fewer than 10 time moments, are pure strategy solvable only by a jitter interval of [-1/18; 2^N-2/3^N-2). The solutions for the one-third progression pattern are compared to the known solutions for the geometrical-progression pattern.

Conclusions. The duel pure strategy solutions obtained suggest a clear one-step-action strategic behaviour in progressive block proposal timing for decentralized consensus protocols under uncertainty of time slots to act. The main benefit is full fairness and a potential reward if the opponent acts non-optimally, even in a single proposal.